抽樣分布

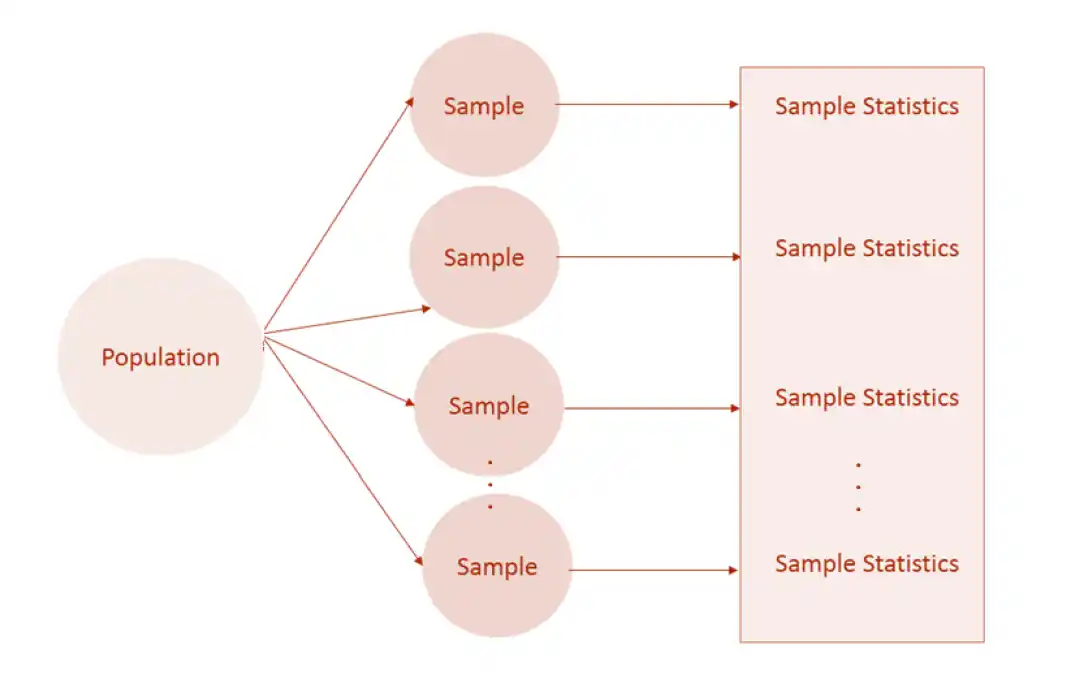
接下會從抽樣分布談到抽樣誤差、信賴區間估計，這裡開始我覺得是真統計的開始。在現實的情況下，我們不會知道一個統計數據母體是什麼分布（如果知道你也不用統計了），通常只有幾組樣本，統計學家會假設一個這次的抽樣結果的統計量（平均數、變異數等等）是從一個「統計結果的統計量」這個母體出來的，事實上你只有一組樣本，但你還是要假設這次抽樣的結果是從很多抽樣結果中抽出來的結果。

知道樣本的抽樣分布是之後對樣本檢定的前置步驟。

提示

統計量

樣本平均數（原$\mu$）：用 $\bar{X}$ 表示，念作 X bar

樣本機率（原$p$）：用 $\hat{p}$，念作 p hat

樣本變異數（原$\sigma^2$）：用 $s^2$ 表示，念做 s 平方

Central Limit Theorem

一個很好用的定理，在樣本夠大（n>30）或已知母體為常態的情況可以直接把統計量的分布看成常態分布

$$\frac{\bar{X}-\mu}{\sigma/\sqrt{n}} \approx N(0,1)$$

• 只需要樣本資訊就可以推估母體
• 不需要母體的任何資訊

平均數（$\bar{X}$）的抽樣分布

• 知道母體平均、變異數的抽樣，可以直接算出樣本的抽樣分布

$$\bar{X}~N(\mu,\frac{\sigma^2}{n})$$ $$Z=\frac{\bar{X}-\mu}{\sigma/\sqrt{n}} \sim N(0,1)$$

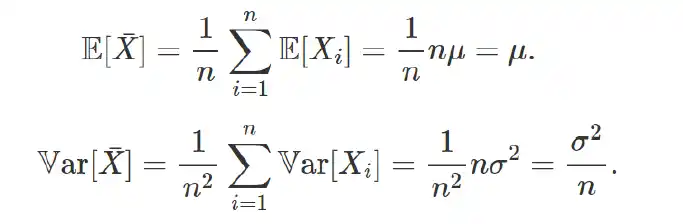
從任何一種分布抽 n 個樣本計算平均後作為新的隨機變數，這個隨機變數的分布就會長得像常態分佈（假設你做了非常多組抽樣，因此才形成一個分布）。

變異數（$s^2$）抽樣分布

變異數抽樣分布會用到卡方分布，這是一個右偏的函數，參數為自由度。從一個常態母體 N(μ, σ²) 中為 n 個樣本，變異數的分布是

$$\frac{(n - 1)s^2}{\sigma^2 }\sim χ²(n - 1)$$

• s² 是樣本變異數
• σ² 是母體變異數
• n 是樣本大小
• χ²(n - 1) 是自由度為 (n - 1) 的卡方分布。卡方念作 chi square，讀音是「ㄎㄞ」

機率（$\hat{p}$）抽樣分布

• p 照抄
• 樣本變異數用 stander error代替
• np>=10 and n(p-1)>=10 ，樣本夠多才能用

$$\mu_{\hat{p}} = p$$ $$SE_{\hat{p}} = \sqrt{\frac{p(1-p)}{n }}$$

提示

stander error(SE)：

這就是離散機率分布中 Bernoulli 的 $\sigma$ ，只是分母多除了樣本數 n。 SE 中文叫做標準誤，它是樣本點估計值的標準差，是對樣本「估計」時產生的誤差大小