跳至主要内容

卡方檢定、獨立性檢定

這個檢定可以拿來估算轉蛋遊戲的機率，很不得早點學會的單元。

就是有個叫做 Weldon 的人覺得骰子六面挖的坑洞數不一樣會讓骰子變的不公平，所以他就手動一直丟骰子想要測試。通常來說就算骰子是公正的，也不可能每丟六次每個數字都分別出現一次，這個檢定就是要測量投擲後和理想次數的差，去查卡方的表（因為種類很少，6 沒有大於 30），決定要不要推翻虛無假設（骰子是公正的）。

卡方檢定​

有兩種狀況，算法其實差不多。根據期望頻率乘上樣本算出理想次數，反正都是和樣本相減平方除上原始期望值後總和算出卡方值。

  • 每個種類期望頻率相同
  • 每個種類期望頻率不同
χ2=∑i=1k(Oi−Ei)2Ei\chi^2 = \sum_{i=1}^{k}{\frac{(O_{i}-E_{i})^2}{E_{i}}}

以六色骰為例，有六個 outcome 所以自由度是 5 。

df=n−1df =n-1

然後拿這個卡方值去查表，但是不用電腦算的話通常沒辦法直接準確的從表格知道確切的 p-value ，好一點的狀況可以寫出區間，如果是這樣也可以反過來查 α\alpha 的卡方值跟加總的卡方值比較就能判斷要不要拒絕 H0H_{0}。

獨立性檢定​

也是個和卡方檢定差不多的東西，不過表格會變成二維，加總算出卡方值會算的很累，最好請出 excel 或統計軟體。

題目就是長這樣的二維表，要你驗證 A、B、C 三個人賣出的東西和他的人是不是獨立（例如A比較會賣產品 1），先算出邊際機率

  • H0H_{0}​：銷售人員與產品類型之間無關（independent）

  • HAH_{A}​：銷售人員與產品類型之間有關（dependent）

df=(row−1)(col−1)df = (row-1)(col-1)

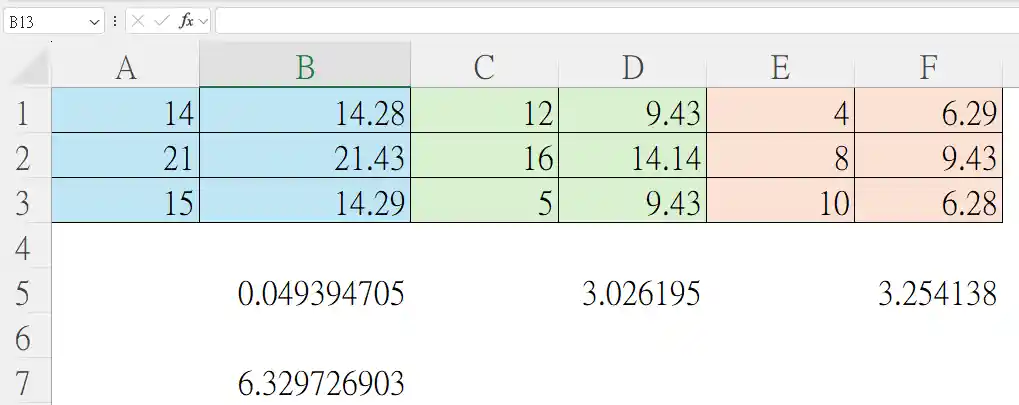
以這題為例，α=0.05\alpha=0.05 查χ0.052(df=4)=9.1488\chi^2_{0.05}(df=4)=9.1488。 excel 算出的卡方值 6.3 比 α\alpha小所以不拒絕虛無假設，暫時接受兩者是獨立的。