ANOVA-變異數分析

這裡講 one-way ANOVA

卡方檢定只能檢查兩個類別的樣本有沒有相同，但到了三組或更多的類別就要用 ANOVA-Analysis of variance。

ANOVA 要算的數字蠻多的，每組計算其實和卡方檢定差不多，大致上都是抓兩組數字相減平方的總和拿去和表格比大小，只不過要算 ANOVA 會算三個名字很像的統計量，一開始只看到這幾個字我也看不是很明白，不過看了過程在幹嘛就會知道了。

• SSG(SSB)-Sum of Square Group/Between
• SSE(SSW)-Sum of Square Error/Within
• SST-Sum of Square Total

例題計算

現在有三組資料($k=3$)，共九個數值($n=9$)，並已經分別算出組平均

G1	G2	G3
3	5	5
2	3	6
1	4	7

$\bar{X}_{1}=2$ $\bar{X}_{2}=4$ $\bar{X}_{3}=6$

$H_{0}：\mu_{1}=\mu_{2}=\mu_{3}$ $H_{A}：$至少存在一組平均與其它組不同

SSG(SSB)

要先算出「全部的」平均 $\bar{X}$，可以全部資料相加再除資料數，或是把 $\sum_{i}^{3}X_{i}/k$

$$SSG=\sum_{i}n_{i}(x_{i}-\bar{x}_{i})^2$$

• 把每組的平均和整體平均做方差，權重是每個組別的資料個數
• 自由度是 $k-1$。

因為只要$\bar{x}_{1}$~$\bar{x}_{3}$ 中少一個也可以透過$\bar{X}$回推

SSE(SSW)

$$SSG=\sum_{i}\sum_{j}(x_{ij}-\bar{x}_{i})^2$$

• 把每一筆資料和對應組平均做方差。
• 自由度是 n-k₁

有些好心的題目會直接把組內的變異數（$s^2$）當成已知，這時候直接把各組變異數分別乘上 $n_{i}-1$ 相加就是 SSE ₂

提示

1. SSW 自由度有人會寫成：組數 X (每組比數-1) ，但這只適用於每組個數都一樣的情況可以列成表格的情況，資料有時候不會這麼完美，用 n-k 比較好。
2. 因為樣本變異數 = $\frac{S_{xx}}{n-1}$ ，這邊我們只要 $S_{xx}$ 也就是方差。

SST

$$SSG=\sum_{i}\sum_{j}(x_{ij}-\bar{x})^2$$

• 每個資料都和總體平均算方差
• 自由度 $n-1$

通常我不會去算這個，因為算完 SSG 、SSW 直接相加就是 SST，自由度也是。

我是跟著這部影片按照步驟算就會了，不同組資料還有顏色區分，挺容易理解的。

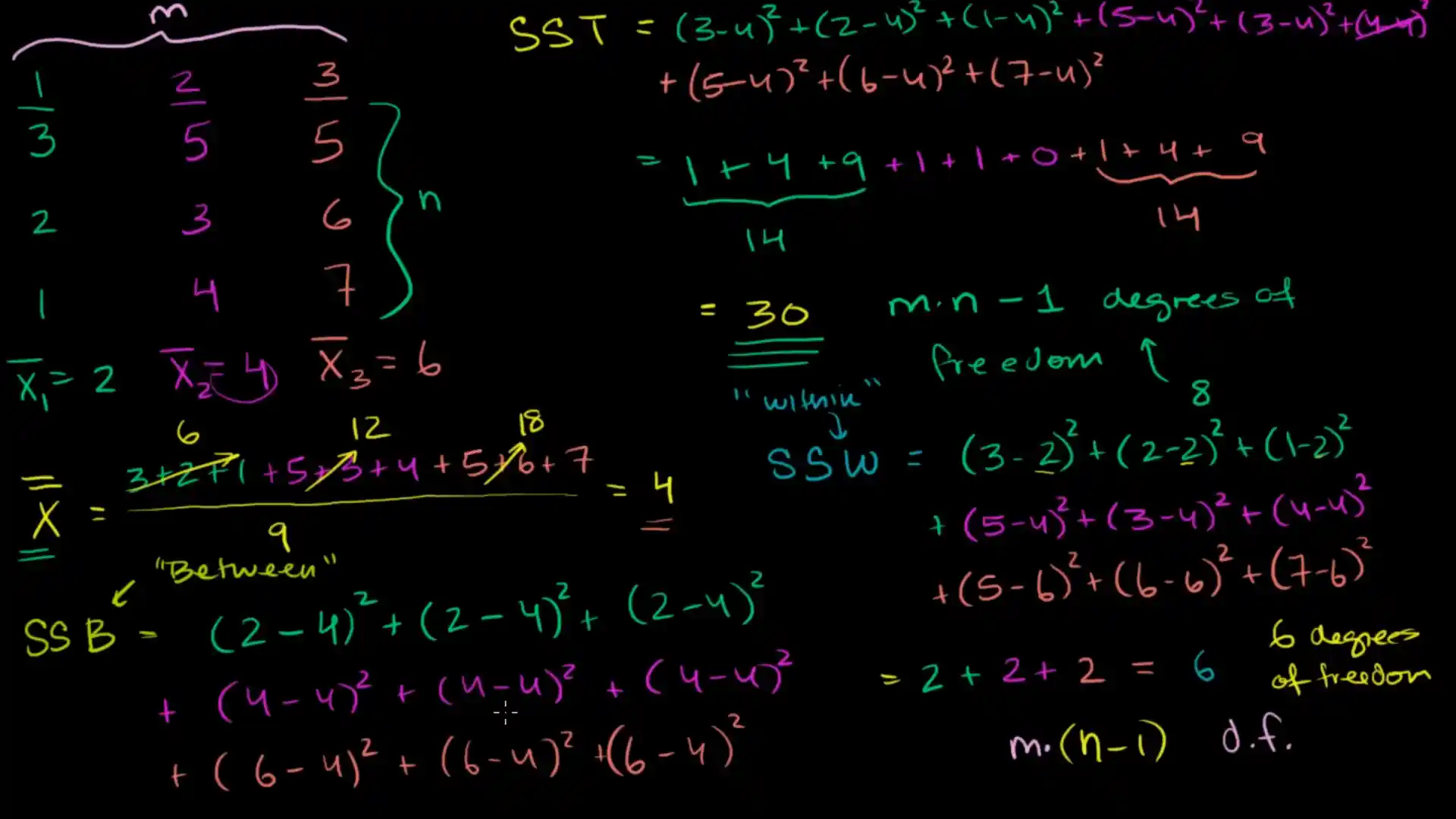
查表

計算：

$F=\frac{\frac{SSB}{k-1}}{\frac{SSE}{n-k}}$

ANOVA 用 F 表，參數是 SSG 和 SSE 的自由度。查出來的值和F做比較，如果F 比較大就 reject $H_{0}$

ANOVA 表格

記好這張表格，你就會算了。

哪裡不一樣？

F 查完如果拒絕的 $H_{0}$ ，只會知道至少存在一組和其他組不同，要找出是哪幾個，要用雙樣本檢定σ₁², σ₂² 已知 且σ₁²≠ σ₂²算 SE

$$SE\sqrt{\frac{MSE}{n_{1}}+\frac{MSE}{n_{2}}}$$

剩下流程和雙樣本比較的時候差不多

• $df=df_{SSE}$
• 去查 T 表得到 p-value
• 重新調整 $\alpha$，變小一點(K 是組數)

$$\alpha*=\frac{\alpha}{\frac{k(k-1)}{2}}$$